I recently encountered the following story on Stack Exchange:
In 1969, D. J. Lewis wrote a paper about Diophantine equations, in which he wrote that the equation \(x^3 + 5 = 117 y^3\) is known to have at most 18 solutions, but the exact number is not known. Two other mathematicians studied the equation and, in 1971, they published a short but difficult proof that there are no solutions. Finally, in 1973, another mathematician found an astonishingly simple proof of the same fact! The proof is:
The quantity \(x^3 + 5\) is never a multiple of 9, but the quantity \(117 y^3\) is always a multiple of 9, so there are no solutions.
I decided to try to verify the short proof at the end of this amusing anecdote. It is easy to show that \(117 y^3\) is always a multiple of 9, because 117 is a multiple of 9. It is somewhat less obvious that \(x^3 + 5\) is never a multiple of 9. This statement is equivalent to \(x^3 \not\equiv 4\ (\text{mod}\ 9)\). I couldn’t come up with an easier way to prove this than just checking all 9 congruence classes individually.
We have:
- \(0^3 \equiv 0\ (\text{mod}\ 9)\)
- \(1^3 \equiv 1\ (\text{mod}\ 9)\)
- \(2^3 \equiv 8\ (\text{mod}\ 9)\)
- \(3^3 \equiv 0\ (\text{mod}\ 9)\)
- \(4^3 \equiv 1\ (\text{mod}\ 9)\)
- \(5^3 \equiv 8\ (\text{mod}\ 9)\)
- \(6^3 \equiv 0\ (\text{mod}\ 9)\)
- \(7^3 \equiv 1\ (\text{mod}\ 9)\)
- \(8^3 \equiv 8\ (\text{mod}\ 9)\)
When I wrote this out, I noticed an interesting pattern. If we evaluate \(a^3\ \text{mod}\ 9\) for \(a = 0,1,2,\dots\), we get a repeating cycle of \([0, 1, 8]\). This made me wonder whether this was a coincidence or if there was something more here. There are of course many well-known theorems about congruences of integer powers, such as Fermat’s little theorem, but I wasn’t familiar with this cyclic behavior.
To look for more general patterns, I wrote a Python script that uses matplotlib to graph the value of \(a^b\ \text{mod}\ m\) for different values of \(a\), \(b\), and \(m\). Each subplot graphs the values of the function for a single \(m\) value. The x-axis is (congruence classes of) \(a\), while the y-axis is \(b\). Columns where \(a\) is coprime to \(m\) are shown in black and white, while columns where \(a\) shares a factor with \(m\) are shown in color. The 3-cycle descibed above is visible as a repeating pattern of 3 colors in the row fourth from the bottom in the plot for \(m = 9\).
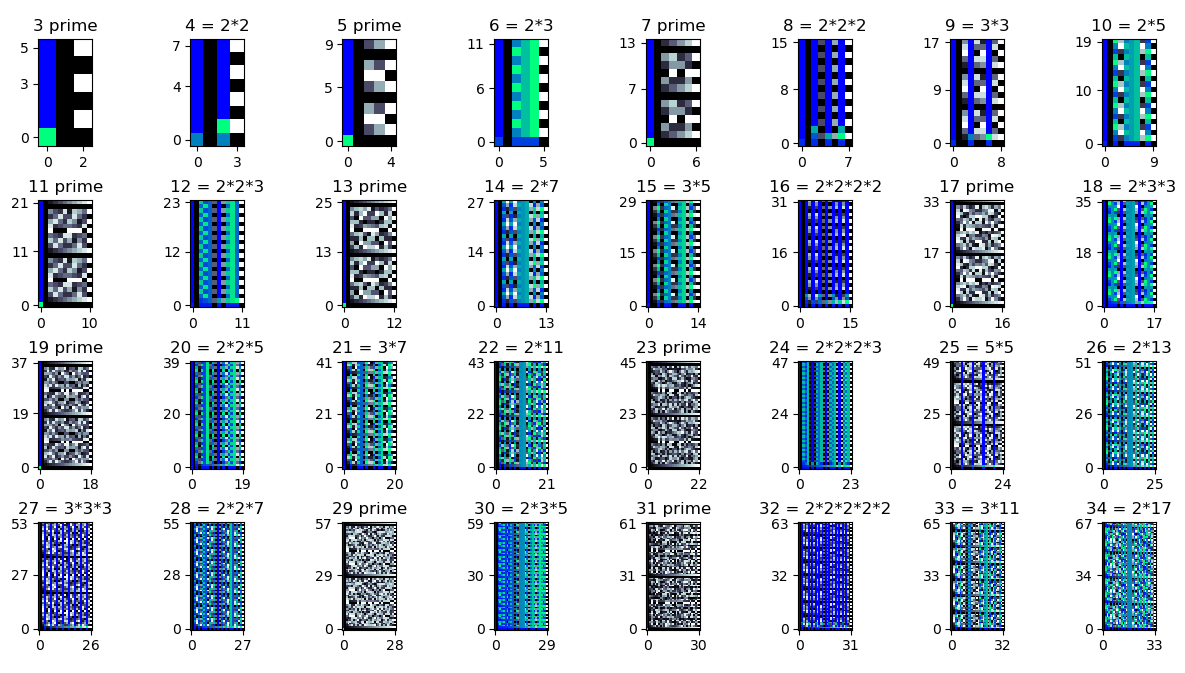
I noticed that there was also a repeating cycle of 5 elements with \(b = 5, m = 25\), similar to the previous repeating cycle with \(b = 3, m = 9\).

As it turns out, this pattern generalizes beyond \(9 = 3^2\) and \(25 = 5^2\). I was able to prove the following:
Theorem: \(a^b\ \text{mod}\ b^2\) is \(b\)-periodic in \(a\). In other words, \((a+b)^b \equiv a^b\ (\text{mod}\ b^2)\).
Proof: By the binomial theorem, \((a + b)^b\) expands into a sum of monomials \[\sum_{k = 0}^{b} \binom{b}{k}\,a^{b - k}\,b^k.\] Any term with \(k \ge 2\) will be divisible by \(b^2\) and hence will not contribute to the final sum. So the final result will be \[\binom{b}{0}\,a^{b - 0}\,b^0 + \binom{b}{1}\,a^{b - 1}\,b^1 = a^b + b\,a^{b - 1}\,b.\] The last term is also divisible by \(b^2\) and hence will not contribute to the final sum. So the final result is just \(a^b\).
Yay, math!